Ohm's Law states that the current through a conductor between two points is directly proportional to the voltage across the two points, and inversely proportional to the resistance between them, provided that the temperature remains constant.
The mathematical equation that describes this relationship is:
In circuit analysis, three equivalent expressions of Ohm's law are used interchangeably:
Kirchoff's Law- are two equalities that deal with theconservation of charge and energy in electrical circuits and were first described in 1845 by Gustav Kirchoff.
Kirchhoff's first rule.
The principle of conservation of electric ccharge implies that:
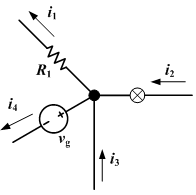
- At any node (junction) in an electrical circuit, the sum of currents flowing into that node is equal to the sum of currents flowing out of that node.
Adopting the convention that every current flowing towards the node is positive and that every current flowing away is negative (or the other way around), this principle can be stated as:
n is the total number of branches with currents flowing towards or away from the node.
This formula is also valid forcomplexcurrents:
The law is based on the conservation of charge whereby the charge (measured in coulombs) is the product of the current (in amperes) and the time (which is measured in seconds).
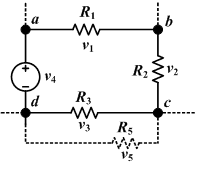
Kirchhoff's voltage law (KVL)
This law is also called Kirchhoff's second law, Kirchhoff's loop (or mesh) rule, and Kirchhoff's second rule.
- The directed sum of the electrical voltage around any closed circuit must be zero.
Similarly to KCL, it can be stated as:
Here, n is the total number of voltages measured. The voltages may also be complex:
This law is based on the conservation of "energy given/taken by potential field" (not including energy taken by dissipation). Given a voltage potential, a charge which has completed a closed loop doesn't gain or lose energy as it has gone back to initial potential level.

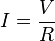

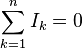
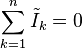

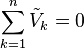
No comments:
Post a Comment